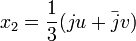معادلة حدودية
في الرياضيات، المعادلات الحدودية أو معادلات متعددات الحدود (بالإنكليزية: Polynomial equations) هي معادلات تأخذ الشكل التالي:

حيث  , معاملات المعادلة, والهدف هو إيجاد جميع قيم المجهول
, معاملات المعادلة, والهدف هو إيجاد جميع قيم المجهول  . ونقول أن كثير الحدود من الدرجة الأولى إذا كانت أعلى قوة ل
. ونقول أن كثير الحدود من الدرجة الأولى إذا كانت أعلى قوة ل  تظهر في المعادلة هي واحد. وهي من الدرجة الثانية إذا كانت أعلى قوة ل
تظهر في المعادلة هي واحد. وهي من الدرجة الثانية إذا كانت أعلى قوة ل  هي اثنين وهكذا دواليك. إذن نقول أن كثيرة الحدود من الدرجة
هي اثنين وهكذا دواليك. إذن نقول أن كثيرة الحدود من الدرجة  إذا كانت أعلى قوة ل
إذا كانت أعلى قوة ل  هي
هي  . وتقول المبرهنة الأساسية في الجبر أن لكل معادلة حدوددية من الدرجة
. وتقول المبرهنة الأساسية في الجبر أن لكل معادلة حدوددية من الدرجة  يوجد عدد
يوجد عدد  من الحلول (ذلك إذا إحتسبنا الحلول المكررة أي التي يجب أن نعدها مرتين). كما تجدر الإشارة إلى أن كل معادلة حدودية ذات معاملات تنتمي إلى الأعداد الحقيقية إن كان لها حلول تنتمي إلى الأعداد المركبة فإن هذه الحلول تكون دائما مترافقة أي أنه يكون دائما هناك حل في شكل
من الحلول (ذلك إذا إحتسبنا الحلول المكررة أي التي يجب أن نعدها مرتين). كما تجدر الإشارة إلى أن كل معادلة حدودية ذات معاملات تنتمي إلى الأعداد الحقيقية إن كان لها حلول تنتمي إلى الأعداد المركبة فإن هذه الحلول تكون دائما مترافقة أي أنه يكون دائما هناك حل في شكل  وآخر في شكل
وآخر في شكل  . أما إذا كانت المعاملات عقدية فإن ذلك ليس صحيحا.
. أما إذا كانت المعاملات عقدية فإن ذلك ليس صحيحا.
 , معاملات المعادلة, والهدف هو إيجاد جميع قيم المجهول
, معاملات المعادلة, والهدف هو إيجاد جميع قيم المجهول  . ونقول أن كثير الحدود من الدرجة الأولى إذا كانت أعلى قوة ل
. ونقول أن كثير الحدود من الدرجة الأولى إذا كانت أعلى قوة ل  تظهر في المعادلة هي واحد. وهي من الدرجة الثانية إذا كانت أعلى قوة ل
تظهر في المعادلة هي واحد. وهي من الدرجة الثانية إذا كانت أعلى قوة ل  هي اثنين وهكذا دواليك. إذن نقول أن كثيرة الحدود من الدرجة
هي اثنين وهكذا دواليك. إذن نقول أن كثيرة الحدود من الدرجة  إذا كانت أعلى قوة ل
إذا كانت أعلى قوة ل  هي
هي  . وتقول المبرهنة الأساسية في الجبر أن لكل معادلة حدوددية من الدرجة
. وتقول المبرهنة الأساسية في الجبر أن لكل معادلة حدوددية من الدرجة  يوجد عدد
يوجد عدد  من الحلول (ذلك إذا إحتسبنا الحلول المكررة أي التي يجب أن نعدها مرتين). كما تجدر الإشارة إلى أن كل معادلة حدودية ذات معاملات تنتمي إلى الأعداد الحقيقية إن كان لها حلول تنتمي إلى الأعداد المركبة فإن هذه الحلول تكون دائما مترافقة أي أنه يكون دائما هناك حل في شكل
من الحلول (ذلك إذا إحتسبنا الحلول المكررة أي التي يجب أن نعدها مرتين). كما تجدر الإشارة إلى أن كل معادلة حدودية ذات معاملات تنتمي إلى الأعداد الحقيقية إن كان لها حلول تنتمي إلى الأعداد المركبة فإن هذه الحلول تكون دائما مترافقة أي أنه يكون دائما هناك حل في شكل  وآخر في شكل
وآخر في شكل  . أما إذا كانت المعاملات عقدية فإن ذلك ليس صحيحا.
. أما إذا كانت المعاملات عقدية فإن ذلك ليس صحيحا.محتويات
توضيح المبرهنة الأساسية في الجبر
إذا اعتبرنا المعادلة التالية:
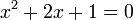
فإن الحل هو ولكن يتم اعتبار هذا الحل مكررا مرتين لأننا يمكن أن نكتب المعادلة بالشكل التالي:
ولكن يتم اعتبار هذا الحل مكررا مرتين لأننا يمكن أن نكتب المعادلة بالشكل التالي:
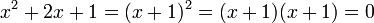
و لذلك نرى أنه لتكون المعادلة صحيحة يجب أن يكون القوس الأول يساوي صفرا أو الثاني يساوي صفرا وفي كل مرة يعينا ذلك حلا أي أن الحل مكرر مرتين. كذلك إذا اعتبرنا
مكرر مرتين. كذلك إذا اعتبرنا
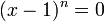
فإن الحل هو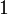 ولكنه مكرر
ولكنه مكرر  مرة إلخ.... بهذه الطريقة تتم حساب عدد الحلول. وعلى أساس ذلك يكون كما هو مذكور أعلاه لكل معادلة حدودية من الدرجة
مرة إلخ.... بهذه الطريقة تتم حساب عدد الحلول. وعلى أساس ذلك يكون كما هو مذكور أعلاه لكل معادلة حدودية من الدرجة  عدد
عدد  من الحلول
من الحلول
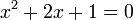
فإن الحل هو
 ولكن يتم اعتبار هذا الحل مكررا مرتين لأننا يمكن أن نكتب المعادلة بالشكل التالي:
ولكن يتم اعتبار هذا الحل مكررا مرتين لأننا يمكن أن نكتب المعادلة بالشكل التالي: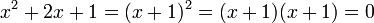
و لذلك نرى أنه لتكون المعادلة صحيحة يجب أن يكون القوس الأول يساوي صفرا أو الثاني يساوي صفرا وفي كل مرة يعينا ذلك حلا أي أن الحل
 مكرر مرتين. كذلك إذا اعتبرنا
مكرر مرتين. كذلك إذا اعتبرنا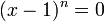
فإن الحل هو
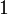 ولكنه مكرر
ولكنه مكرر  مرة إلخ.... بهذه الطريقة تتم حساب عدد الحلول. وعلى أساس ذلك يكون كما هو مذكور أعلاه لكل معادلة حدودية من الدرجة
مرة إلخ.... بهذه الطريقة تتم حساب عدد الحلول. وعلى أساس ذلك يكون كما هو مذكور أعلاه لكل معادلة حدودية من الدرجة  عدد
عدد  من الحلول
من الحلولطرق حل معادلات كثيرة الحدود]
المعادلة من الدرجة الأولى]
حل المعادلة:  هو
هو  حيث
حيث 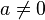 ونستطيع حل معادلات الدرجة الأولى بكل سهولة فمثلا:- مثال 1:- حل المعادلة التالية س+5=10 الحل:- س+5-5=10-5 وبالاختصار نجد أن:- س=5 بحيث لو عوضنا بقيمة س نحصل على الناتج 10 5+5=10 وهناك طريقة أخرى وهي نقل الحد الثاني إلى الجهة الأخرى بعكس إشارته. س=10-5 س=5
ونستطيع حل معادلات الدرجة الأولى بكل سهولة فمثلا:- مثال 1:- حل المعادلة التالية س+5=10 الحل:- س+5-5=10-5 وبالاختصار نجد أن:- س=5 بحيث لو عوضنا بقيمة س نحصل على الناتج 10 5+5=10 وهناك طريقة أخرى وهي نقل الحد الثاني إلى الجهة الأخرى بعكس إشارته. س=10-5 س=5
 هو
هو  حيث
حيث 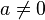 ونستطيع حل معادلات الدرجة الأولى بكل سهولة فمثلا:- مثال 1:- حل المعادلة التالية س+5=10 الحل:- س+5-5=10-5 وبالاختصار نجد أن:- س=5 بحيث لو عوضنا بقيمة س نحصل على الناتج 10 5+5=10 وهناك طريقة أخرى وهي نقل الحد الثاني إلى الجهة الأخرى بعكس إشارته. س=10-5 س=5
ونستطيع حل معادلات الدرجة الأولى بكل سهولة فمثلا:- مثال 1:- حل المعادلة التالية س+5=10 الحل:- س+5-5=10-5 وبالاختصار نجد أن:- س=5 بحيث لو عوضنا بقيمة س نحصل على الناتج 10 5+5=10 وهناك طريقة أخرى وهي نقل الحد الثاني إلى الجهة الأخرى بعكس إشارته. س=10-5 س=5المعادلة من الدرجة الثانية]
لحل المعادلة:  , نحسب المميز
, نحسب المميز  المعرف ب:
المعرف ب:  , ويكون للمعادلة حلان هما:
, ويكون للمعادلة حلان هما:
 , نحسب المميز
, نحسب المميز  المعرف ب:
المعرف ب:  , ويكون للمعادلة حلان هما:
, ويكون للمعادلة حلان هما:
 .
.
المعادلة من الدرجة الثالثة]
 طالع أيضًا: دالة_تكعيبية#صيغة_غاردان
طالع أيضًا: دالة_تكعيبية#صيغة_غاردان
طريقة كاردان]
طريقة كاردان هي طريقة تمكن من حل جميع المعادلات من الدرجة الثالثة.
هذه الطريقة تكمن من استعمال صيغ كاردان المعطات بدلالة  و
و حلول المعادلة:
حلول المعادلة:  . وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا.
. وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا.
 و
و حلول المعادلة:
حلول المعادلة:  . وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا.
. وهي تمكن من البرهنة على أن المعادلات من الدرجة 3 يمكن حلها جبريا.صيغ كاردان
بالنسبة للمعادلة:  نحسب
نحسب  , ثم ندرس إشارته.
, ثم ندرس إشارته.
 نحسب
نحسب  , ثم ندرس إشارته.
, ثم ندرس إشارته.Δ موجب]
نضع
الحل الوحيد الحقيقي هو 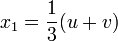 .
.
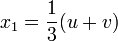 .
.
و حلان عقديان مترافقان:
حيث 

Δ سالب[عدل]
يوجد عدد عقدي u الذي هو جذر مكعب ل  .
.
 .
.
المعادلة تقبل ثلاث حلول حقيقية:
تفسير الطريقة[عدل]
الصيغة المختصرة[عدل]
نعتبر الصيغة العامة للمعادلة:  ,
,
 ,
,
نضع:

لنحصل على الصيغة:

نضع الآن:
 الآن نحصل على مجهولين بدل مجهول واحد, لكن نضع شرطا يمكن من التبسيط:
الآن نحصل على مجهولين بدل مجهول واحد, لكن نضع شرطا يمكن من التبسيط:
 تتحول هذه المعادلة إلى الشكل:
تتحول هذه المعادلة إلى الشكل:
 شرط التبسيط يكون إذن:
شرط التبسيط يكون إذن:
 الذي يعطي من جهة:
الذي يعطي من جهة:
 و من جهة أخرى:
و من جهة أخرى:
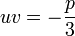 و عند رفع العددين إلى القوة 3, نحصل على:
و عند رفع العددين إلى القوة 3, نحصل على:
 و نحصل أخيرا على نظمة معادلتين لمجهولين
و نحصل أخيرا على نظمة معادلتين لمجهولين  و
و الآتية :
الآتية :


 و
و هما إذن عددين نعرف جمعهما وجذاءهما. هذين العددين هما جذرا المعادلة من الدرجة الثانية:
هما إذن عددين نعرف جمعهما وجذاءهما. هذين العددين هما جذرا المعادلة من الدرجة الثانية:


لنحصل على الصيغة:

نضع الآن:
 الآن نحصل على مجهولين بدل مجهول واحد, لكن نضع شرطا يمكن من التبسيط:
الآن نحصل على مجهولين بدل مجهول واحد, لكن نضع شرطا يمكن من التبسيط: تتحول هذه المعادلة إلى الشكل:
تتحول هذه المعادلة إلى الشكل: شرط التبسيط يكون إذن:
شرط التبسيط يكون إذن: الذي يعطي من جهة:
الذي يعطي من جهة: و من جهة أخرى:
و من جهة أخرى: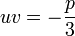 و عند رفع العددين إلى القوة 3, نحصل على:
و عند رفع العددين إلى القوة 3, نحصل على: و نحصل أخيرا على نظمة معادلتين لمجهولين
و نحصل أخيرا على نظمة معادلتين لمجهولين  و
و الآتية :
الآتية :

 و
و هما إذن عددين نعرف جمعهما وجذاءهما. هذين العددين هما جذرا المعادلة من الدرجة الثانية:
هما إذن عددين نعرف جمعهما وجذاءهما. هذين العددين هما جذرا المعادلة من الدرجة الثانية:
المعادلة من الدرجة الرابعة
طريقة فيراري
نعتبر الصيغة العامة للمعادلة من الدرجة الرابعة: 

نقسم على  ونضع
ونضع
 ونضع
ونضع
لنصل إلى معادلة على صيغة :

معادلة تكتب:

نضيف

لطرفي المتساوية. فنحصل على:

نلاحظ أن الطرف الأول يكتب على صيغة مربع:

من هاته النتيجة الأخيرة, نقوم بالنشر :


 (*)
(*)
الهدف هو تحديد y بحيث يكتب الطرف الثاني أيضا على صيغة مربع.
الطرف الثاني معادلة من الدرجة الثانية  . يكتب على شكل مربع. إذا كان المميز منعدما يعني:
. يكتب على شكل مربع. إذا كان المميز منعدما يعني:
 . يكتب على شكل مربع. إذا كان المميز منعدما يعني:
. يكتب على شكل مربع. إذا كان المميز منعدما يعني:
الشيء الذي يعطي, عن طريق النشر والتجميع معادلة من الدرجة الثالثة  الآتية :
الآتية :
 الآتية :
الآتية :
نستطيع حل هذه المعادلة باستعمال الطريقة الخاصة بمعادلات الدرجة الثالثة لإيجاد  .
.
 .
.![u = \sqrt[3]{\frac{-27q + 3\sqrt{3}\sqrt{\Delta}}{2}}](https://upload.wikimedia.org/math/e/7/6/e76173bddab23ed6f1463eeadfba1f63.png)
![v = \sqrt[3]{\frac{-27q - 3\sqrt{3}\sqrt{\Delta}}{2}}](https://upload.wikimedia.org/math/8/8/5/885e4b9cd087bc15ba9481b8d78d96e7.png)